Döngüler Neden Kullanılır?
Programlama dillerinde döngüler, önemli bir yere sahiptir. Kod yazarken çok ama çok uzun bir satırı döngüler sayesinde çok daha kısa bir şekilde yazabilmek mümkündür. Örneğin;
16F877A Pic mikrodenetleyicisinin C portuna bağlı olan çıkışlarına sırasıyla 0'dan 9'a kadar olan sayıları döngü kullanmadan yazalım.
---------------------------------------------------------
int x=0;
output_c(x); //C portuna 0 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 1 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 2 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 3 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 4 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 5 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 6 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 7 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 8 değeri gönderildi.
x++;
delay_ms(500);
output_c(x); //C portuna 9 değeri gönderildi.
x++;
delay_ms(500);
--------------------------------------------------------------
Yukarıdaki kodlarla 0'dan 9'a kadar olan sayılar yaklaşık 30 satırla döngü olmadan tamamlandı.
C portuna 0'dan 9'a kadar olan sayıları yazdıran programı döngü kullanarak aşağıdaki şekilde yazabiliriz:
----------------------------
for(int i=0;i<10;++i)
{
output_c(i);
delay_ms(500);
}
-----------------------------
İşte bu kadar. Evet 5 satırlık kodlar istenilen işlemler for döngüsü kullanılarak gerçekleştirildi. Döngüler bu örnekteki gibi pek çok işlemi gerçekleştirmemize olanak sağlar.
Şimdi bu döngüleri sırasıyla tanıyalım;
1- For Döngüsü
For döngüsünde belli bir sayıdan başlayarak bir işlemi istenilen sayıda tekrar edilir. For döngüsünün yapısı şu şekildedir;
for(ilk değer; koşul; yapılacaklar)
{
işlemler
}
örnek1:16f877A entegresi kullanarak denetleyicinin A portuna bağlı olan pinlere 0'dan 5' e kadar olan sayılar atılacaktır. Gerekli programı yazınız.
çözüm:
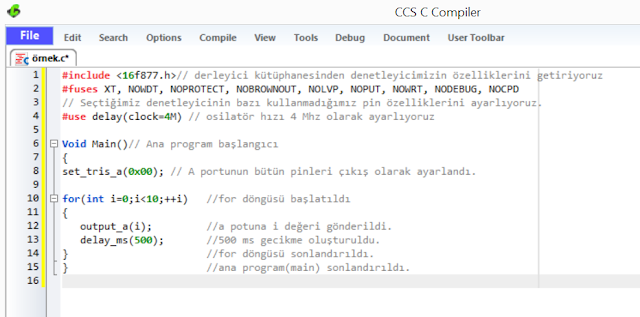 |
| şekil 1 |
Şekil 1'de for döngüsünün kullanımıyla ilgili örnek yer almaktadır. 9. satırda for döngüsü başlatılmaktadır. Bu örnekte for döngüsünün açıklaması şöyledir:
- Başlangıç değeri 0 olan bir i değişkeni tanımlanır.
- i sayısının 10 küçük olup olmadığı kontrol edilir.
- Eğer i sayısı 10'dan küçükse i değeri 1 artırılır.
- i değişkeni 10 dan küçük olduuğu sürece parantez içerisindeki işlemler devam eder.
- i değişkeni 10 olduğu zaman döngüden çıkılır.
- Döngüde i sayısı sırasıyla 0,1,2,3,4,5,6,7,8,9 değerlerini alır ve a portuna sırasıyla bu değerler output_a(i); komutuyla gönderilir.
2- While Döngüsü
While döngüsü aslında bir koşul döngüsüdür. Bu döngüyle bir şartın olup olmadığı kontrol edilir. Eğer istenilen şart sağlanırsa döngünün içerisindeki satırlar işletilir. Şart sağlanmaz ise döngüden çıkılır.
While döngüsünün kullanımı şöyledir;
while(koşul ifadesi)
{
işlemler
}
örnek2: x adında sabit bir değişken tanımlansın. x değeri 0.5 saniye aralıklarla 1 artsın ve bu artış x değeri 10 olana kadar devam etsin ve bu arada b portuna bağlı ledler 100 ms aralıklarla yanıp sönsün. x değeri 10 olduğunda döngüden çıkılsın. Gerekli programın kodlarını yazınız?
çözüm:
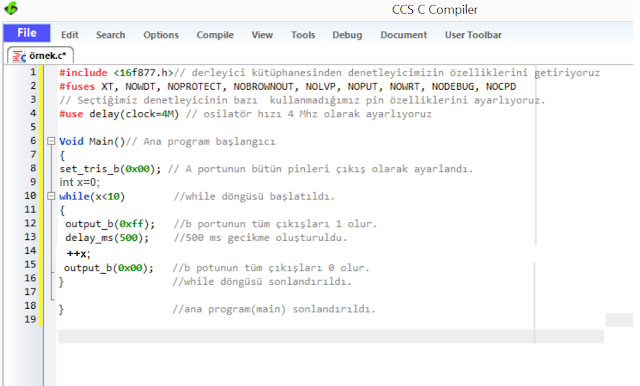 |
| şekil 2 |
Şekil 2'deki çözümde while döngüsünün kullanımıyla ilgili çözüm yer almaktadır. Örnekte while döngüsü 10. satırdan başlamaktadır. Örnekte döngünün kullanımı şöyledir:
- 10. satırdaki koşulda x'in 10'dan küçük olup olmadığı kontrol ediliyor.
- x değişkeni 10'dan küçük olduğu sürece while döngüsü 10. ve 15. satırlar arasında işletilir. x'in 10 dan küçük olduğu durumlarda x sırasıyla 0,1,2,3,4,5,6,7,8,9 değerlerini alır ve her değerde b portuna bağlı ledler 500 ms aralıklarla yanıp söner.
- x değişkeni 10 olduğu anda döngüden çıkılır.
- 18. satırda ise ana program sonlandırılır.
3-Do-While Döngüsü
Do While döngüsü while döngüsüyle aynı işlevi görür. Do-While döngüsünün kullanımı şöyledir;
do
{
işlemler
}while(koşul ifadesi);
Örnek2' deki soru do-while döngüsüyle şu şekilde çözülür:
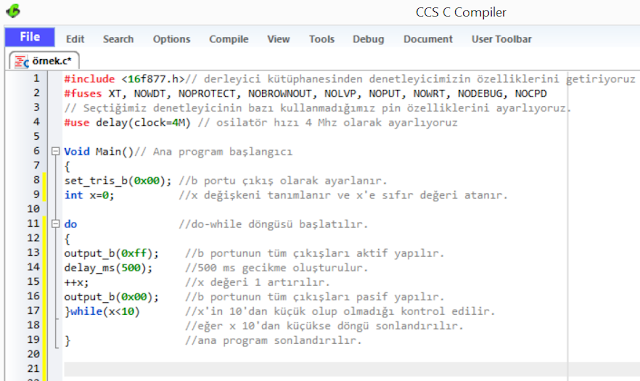 |
| şekil 3 |
şekil 3'de do-while döngüsüyle ilgili örnek çözüm yer almaktadır. Örneğe bakacak olursak;
- 17. satırda x sayısının 10'dan küçük olup olmadığı kontrol edilir. Eğer x 10'dan küçükse do-while döngüsü içerisindeki işlemler gerçekleştirilir yani 12 ve 17. satırlar arasındaki satırlar işletilir.
- x sayısı 10 olduğunda ise döngüden çıkılır ve program 19. satırda sonlandırılır.
4-Sonsuz Döngüler
Sonsuz döngüler, programlamada bir işin sürekli yapılması istenilen durumlarda kullanılır. Sonsuz döngü içerisindeki ifadeler sürekli tekrarlanır. Yani sürekli aynı işlemler yapılır.
örnek3: mikrodenetleyicinin b portuna bağlı olan ledler 1 saniye aralıklarla sürekli yanıp sönsün. Gerekli kodları yazınız.
Sonsuz döngüler while, do-while ve for döngüleriyle oluşturulabilir.
- while döngüsü sonsuz döngü olarak şu şekilde oluşturulur:
while(1)
{
işlemler
}
- do-while döngüsü sonsuz döngü olarak şu şekilde oluşturulur:
do
{
işlemler
}while(1)
- for döngüsü sonsuz döngü olarak şu şekilde oluşturulur:
for(;;)
{
işlemler
}
örnek3, while sonsuz döngüsüyle şu şekilde oluşturulur(şekil 4);
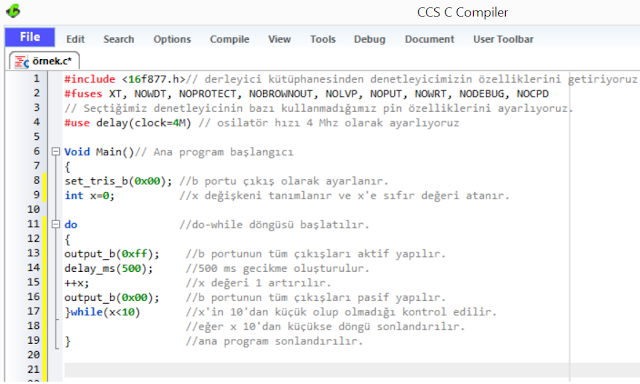 |
| şekil 4 |
örnek3, do-while sonsuz döngüsüyle şu şekilde oluşturulur(şekil 5);
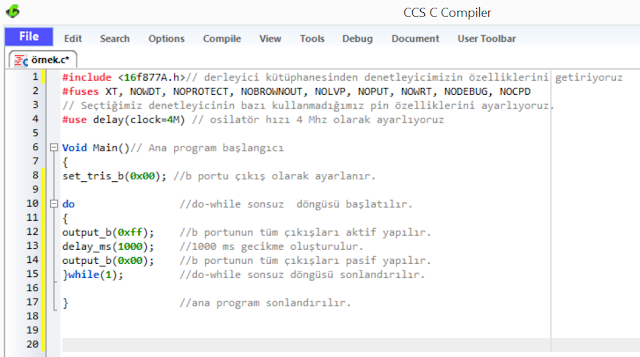 |
| şekil 5 |
örnek3, for sonsuz döngüsüyle şu şekilde oluşturulur(şekil 6);
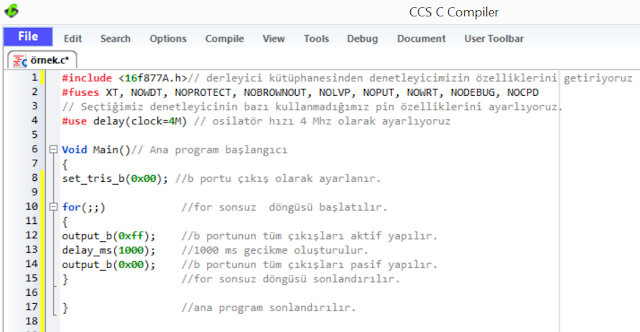 |
| şekil 6 |